Diario 6 / L’albero di Calkin Wilf
Sono giorni complessi, per tutti. Da qualche tempo però una strana sensazione si è fatta largo tra i mille impegni di una scuola d’emergenza; l’idea che i drammatici eventi di questi mesi non abbiano cancellato tutto, che ci siano ancora altri dolori e altre lacrime che non possiamo abbandonare. Ma anche tante piccole cose belle, il quotidiano stupore, la poesia, la matematica. Quale parte ho in tutto questo? Come educatore, come padre, forse anche come cittadino. Allora il dubbio, premessa di ogni ragionamento: forse il mio ruolo richiede anche (non solo) di tornare a parlare di vita in un mondo circondato quotidianamente dalla morte. Per stanchezza, ma a questo punto credo anche per dovere, ho pensato dunque di usare questo spazio per esplorare, brevemente e in modo incerto, altro. Di staccare le parole dal reale e, per una volta soltanto, condividere una storia diversa. Di scuola, certo, perché questo è il mio mestiere. Di matematica, sicuramente, perché mi manca parlarne. Un incontro in sala insegnanti di un mercoledì d’ottobre in una delle poche ore buche di questa ripartenza accidentata. Non sono nemmeno sicuro che sia successo davvero, rimane un ricordo a metà per questo diario a metà. Il reale, o la mancanza di reale, non è mai stato d’impedimento, credo valga anche in questo caso.
Le coordinate spaziotemporali sono certe, una pausa tra le lezioni in una sala insegnanti vuota, il non luogo universale di ogni scuola. Sono sicuro fosse la terza ora perché ho firmato il registro d’ingresso (massimo 10 persone alla volta avverte ancora il cartello sulla porta), ho disinfettato le mani e mi sono seduto mascherato nel mio angolo preferito. Un’ora buca è rara di questi tempi, avevo bisogno di ripensare alla lezione per la prima, dovevo limare parole e idee, teoremi e dimostrazioni. Testimoni il quaderno aperto sul tavolo di fronte, le penne allineate in una delle mie tante ossessioni geometriche, la musica a eliminare il mondo dalle mie orecchie. E mentre Rael cercava di convincermi con i suoi sogni a dargli una mano per trovare la porta d’uscita, ho iniziato a contare i cassetti. Lo faccio spesso quando sono in pausa, allineati contro una parete sono la perfetta rappresentazione dell’insegnante. Un cassetto esatto per ognuno e ognuna di noi, una corrispondenza biunivoca segnata da gialle targhette con i nomi. Ad ogni insegnante corrisponde uno ed un solo cassetto; e viceversa. I matematici la chiamano biezione e ci permette di dire una cosa banale, i cassetti e gli insegnanti esistono nello stesso numero (nomine di supplenti a parte). Sarà stata la musica insistente, o forse l’ombra di una giornata di pioggia, ma in quell’ora buca, il quaderno ancora intonso, i cassetti sembravano infiniti.
Che scuola affollata sarebbe, ho pensato. Un cassetto per ogni insegnante, infiniti gli uni e gli altri. E se poi arriva un supplente all’ultimo minuto? Come fa senza cassetto? Sono tutti occupati. Hilbert, anni fa, ci ha spiegato che non è un problema, sposto le cose del cassetto del primo collega nel cassetto del secondo collega, quelle del secondo cassetto nel terzo, quelle del terzo nel quarto e così via. Tutti si spostano, ma tutti hanno ancora un cassetto, anche il nuovo supplente (che è pure simpatico) che si ritrova il primo cassetto libero. Provo a farlo, tanto ho tutta l’ora; solo che i cassetti non sono infiniti, sono 112 e la cosa in questo caso non funziona, alla fine ho liberato il primo ma tutta la roba dell’ultimo non so dove metterla. Stern sarà furiosa, spero sia il suo giorno libero. La sua roba la metto nel primo cassetto ormai vuoto, la targhetta dice Brocot, ma non importa, la biezione funziona ancora. Certo, adesso i colleghi non troveranno più le loro cose (i compiti, i libri, le lime e gli atlanti, direbbe qualcuno), ma in fondo è solo una delle tante permutazioni dei cassetti; con 112, se le volessi fare tutte, sarebbero un numero con 183 cifre, non penso sia il caso se voglio finire di preparare la lezione per la prima.
La musica nel frattempo è cambiata, adesso una voce insiste nel dirmi che il tempo è dalla sua parte; non ne dubito, ma non dalla mia, lo spostamento inutile dei cassetti mi ha fatto perdere buona parte dell’ora buca ricordandomi che il privilegio degli insiemi infiniti è precluso a noi creature finite. Ed è esattamente in quell’istante che mi sono accorto di non essere solo. Non avevo notato il collega seduto in fondo alla sala, elegante e silenzioso senza mascherina (sarà abbastanza lontano?), la mano appoggiata all’avorio di un bastone da passeggio, lo sguardo appeso al soffitto. Il volto mi era in qualche modo familiare senza però la connotazione precisa di un nome. Che figura, è stata la prima cosa che ho pensato, chissà che avrà pensato del mio tentativo di trasloco alla Hilbert dei cassetti. Solo più tardi, tornato a casa, ho ricordato la mancanza della sua firma sul registro, lo sguardo liquido, l’età piuttosto avanzata. E poi, chi va in giro con un bastone da passeggio di questi tempi? Con manico d’avorio (o forse plastica)? Un supplente senza cassetto? Troppo anziano persino per un paese ingrato verso i precari della scuola come il nostro.
Un rappresentante di testi scolastici? Impossibile di questi tempi dove la carta sembra uno schermo di serie B. Ripensando alla carta, sono tornato al mio quaderno e alla sua pagina aperta e vuota da più di mezz’ora. Come atto di gentilezza ho tolto gli auricolari, un conto è escludere il mondo, un altro è essere sgarbati con qualcuno con cui dividiamo luoghi e tempi. Ho accennato un saluto ottenendo in cambio un ampio sorriso luminoso, la testa dello sconosciuto leggermente inclinata verso l’alto e lo sguardo appeso al solito punto distante. “Lei si occupa di matematica?” mi ha chiesto con voce sussurrata, sempre senza guardarmi. Ho risposto un po’ a disagio che insegnare matematica non è la stessa cosa che occuparsi di matematica; chi se ne occupa costruisce palazzi e città, edifica nazioni ed imperi, io mi limito a fare la guida turistica. “Però insegnando matematica forse può aiutarmi.”. Ecco, ricordo d’aver pensato, questo è il solito collega di lettere che adesso mi appioppa un assurdo calcolo della rata del mutuo o del premio dell’assicurazione che non lo convince. Non mi dovete chiedere i calcoli, quella non è matematica, è burocrazia del numero. Stavo quasi per inventarmi una scusa, tipo dover rimettere in ordine i cassetti prima che Stern si accorga dello scambio con Brocot, ma la curiosità per quello strano individuo seduto a gambe larghe ad osservare il soffitto mi spinse a rispondere un poco convinto “Se posso…”.
Il suo sorriso divenne, se possibile, ancora più largo. “Mi chiedo se lei possa gentilmente indicarmi come contare le frazioni.”. La domanda sembrava strana se non altro perché era esattamente l’argomento che dovevo preparare per l’ora successiva in prima. Mi avrà visto spostare i cassetti, ho pensato. “Vede, l’ho vista spostare i cassetti” – lo sapevo – “e mi ha fatto tornare in mente il gioco di Hilbert, sono sicuro che lei lo conosce. Ho pensato spesso all’infinito numero dei numeri, mi sono convinto di tutto quel che voi ci insegnate, ma mi è rimasto un dubbio di fondo; contare cassetti (e insegnanti di conseguenza) è facile, ma come conto le frazioni?”. Risposi che sono infinite, proprio come i numeri interi. “Ecco il punto in cui il mio orizzonte vacilla" rispose lui velocemente, “provi a seguire l’incertezza del mio passo anziano. Supponiamo che io disponga in fila tutte le frazioni (limitiamoci a quelle positive, il discorso non cambia) partendo da quelle che hanno al numeratore 1. Dunque 1/1 1/2 1/3 1/4 e a seguire tutte le altre. Una per ciascun numero intero, vede, le posso contare con i numeri che ci sono al denominatore. La frazione numero 1, la frazione numero 2, la numero 3 e così via.”. Risposi che mi sembrava ragionevole. “Questo ci porta dritti al mio inciampo” proseguì l’uomo dal bastone inseparabile.
“Perché io non potrò mai finire questa riga di frazioni, esse sono tante quante tutti i numeri che sono infiniti, come i cassetti dei suoi infiniti colleghi a cui lei pensava poco fa. E nonostante questo loro essere infiniti, stiamo lasciando fuori tutte le altre frazioni, quelle che non hanno 1 al numeratore, come 2/3 o 7/5”. Non chiesi come faceva a sapere del mio sogno di cassetti infiniti di prima (un piccolo interstizio di assurdità direbbe qualcuno), ma volli provare a spiegare la cosa. “Vede, questa sua disposizione, per quanto legittima, non è ottimale e possiede almeno due difetti. Il primo è che, come lei ha sottolineato, induce a pensare che le frazioni siano molte di più dei numeri interi (limitandoci ai positivi dovrei parlare di numeri naturali e non di interi, ma non sottilizziamo). Il secondo è che se proseguo con la sua idea e sviluppo una seconda riga, ottengo molte (infinite) ripetizioni.”
“In che senso?”
“La seconda riga di frazioni dovrebbe essere fatta da 2/1 2/2 2/3 2/4 e così via. Vede subito che la seconda frazione di questa sequenza, 2/2, è equivalente a 1/1 che già apparteneva alle frazioni che lei ha riportato in precedenza. E anche la frazione 2/4 è già stata nominata, è, come spero converrà, del tutto equivalente a 1/2. Le lascio intuire che di queste ripetizioni ce ne sono infinite. E anche nelle sequenze successive, quelle che contengono le frazioni con numeratore 3, con numeratore 4 etc. Riassumendo questa disposizione ha due difetti: induce falsamente a pensare che siccome ogni riga è in corrispondenza con gli infiniti interi e di righe di frazioni ce ne sono infinite, le frazioni siano molte di più degli interi. In secondo luogo questa rappresentazione contiene tantissimi (infiniti) doppioni.”
“In effetti non ci avevo pensato. Ma io so che Cantor ha usato esattamente questa disposizione nei suoi lavori.”
“Oh, conosce Georg Cantor? Che bello, non è facile trovare qualcuno con cui parlarne qui a scuola. In ogni caso è vero, Cantor usò proprio una costruzione di questo tipo per discutere іl problema di contare le frazioni, ma esiste un’alternativa che a mio modo di vedere è preferibile.”
“Ed è qualcosa che anche un vecchio dromomane come me può capire?”
“Certo, basta usare un albero!”
“Mi perdoni, ma io qui vedo, o indovino dalle ombre, cassetti, un tavolo, delle sedie, un quaderno (con la pagina ancora bianca e intonsa, scusi se lo noto), delle penne e noi due, non intuisco alberi. Vuole che ci spostiamo in giardino? Nel caso dovrà darmi una mano, l’età e la vista non mi consentono di spostarmi da solo in luoghi che non conosco.”
“Mi scuso per il malinteso, intendevo alberi in senso matematico, sono costruzioni molto belle, quasi dei labirinti.”
“Belli i labirinti, mi sono sempre piaciuti sin da ragazzo! Continui, la prego.”
“L’idea è piuttosto semplice, anche se per le dimostrazioni ci vuole un po’ di pazienza; ma se vuole le risparmio i dettagli e arrivo subito alla costruzione. Immagini di avere una generica frazione a/b. Bene, a questa frazione ne attacchiamo idealmente altre due ottenute con una regola semplice; a sinistra mettiamo una nuova frazione in cui sostituiamo il denominatore con la somma di numeratore e denominatore, a destra facciamo la stessa cosa, ma sostituendo il numeratore. In simboli le due nuove frazioni sono a/(a+b) e (a+b)/b. Mi segue?”
“Ci provo, ma scriva più grande per favore. Sa, la vista di un vecchio.”
“Scusi. Adesso arriviamo all’albero: applichiamo ricorsivamente questa regola partendo dalla prima frazione, 1/1 e poi continuando su ogni nuova frazione che viene fuori. Si ottiene qualcosa di simile alla figura. Spero sia abbastanza grande.”
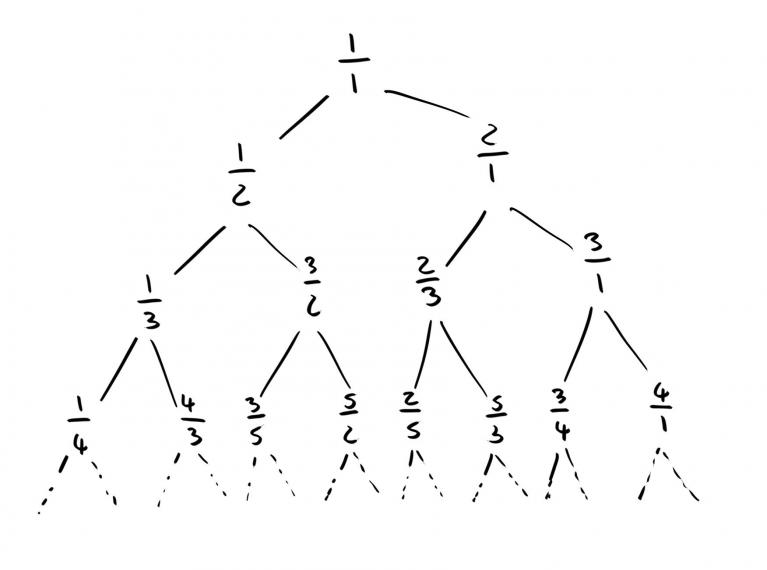
“Sì, lo è. E questa costruzione quando si ferma?”
“Mai, prosegue all’infinito. La struttura che ne vien fuori si chiama albero di Calkin-Wilf e indovini un po’? Contiene esattamente tutte le frazioni. Ovviamente solo quelle positive, ma si può estendere il discorso per includere anche quelle negative.”
“Lei mi sta dicendo che questa specie di labirinto in cui in ogni stanza si affacciano due nuove stanze (mi ricorda qualcosa che scrissi tanti anni fa) contiene tutte le frazioni? Ne è sicuro?”
“Assolutamente, lo posso dimostrare. Posso anche dimostrare che ciascuna frazione compare esattamente una volta sola in tutto l’albero. E sono sicuro che noterà molte proprietà e simmetrie di questa costruzione, le basta un foglio e una penna (e un po’ di tempo). Vuol vedere qualche dimostrazione?”
“No no, mi fido, per carità. E questo albero (mi torna in mente l’albero nel cortile della mia casa paterna, lo guardavo ogni giorno dallo studio di mio padre mentre ero immerso nella lettura di Melville e de Quincey) ci aiuta a contare le frazioni?”
“Certo. Perché è facile mostrare un secondo albero, identico in struttura a questo (si dicono entrambi binari) che contiene però i numeri interi. Eccolo qui, penso che la costruzione parli da sola.”
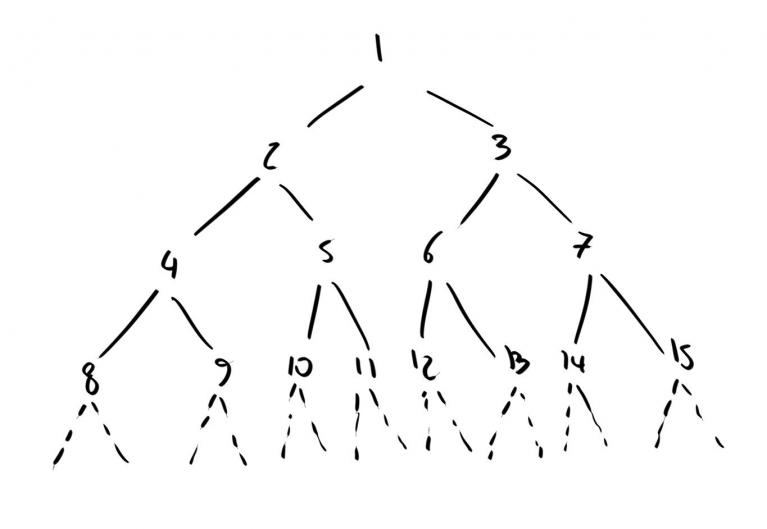
Il mio interlocutore si fermò a guardare i miei scarabocchi senza guardarli davvero. Lo sentii mormorare qualcosa riguardo gli specchi, quasi impaurito. “Dunque le frazioni sono tante quante gli interi, ora lo vedo; questi due palazzi dai corridoi precisi come cristalli combaciano perfettamente, ad ogni stanza di uno corrisponde esattamente una stanza dell’altro, e viceversa. Un po’ come i cassetti con gli insegnanti.”
“Esatto. Tutte cose già dimostrate e previste da Cantor, ma questa rappresentazione grafica dei numeri ha il vantaggio dell’immediatezza.”
“Come le ho accennato prima, Cantor lo conosco bene, ho letto di lui nei libri di Bertrand Russell. O era viceversa? La mia memoria di vecchio è a sua volta un labirinto. Però la ringrazio, questa costruzione illuminante non l’avevo mai vista. Immagino sia un bene che queste cose si facciano ora a scuola.”. Risposi di non esserne certo, avrei voluto provare quella mattina stessa a sviluppare l’argomento nella mia prima, era un esperimento fuori dai programmi e dai libri, un primo passo per poi estendere il discorso ad altri numeri ancora più complessi, altri infiniti da esplorare. Mi sorrise senza guardarmi “Vedo che anche lei si sta perdendo. Forse è un bene. Ma stia attento alla bestia che c’è nel cuore di ogni labirinto, è inevitabile come il tempo e lo spazio. O l’ombra.”
Fu in quel momento che la campanella suonò. Alzai la testa dal tavolo mentre dagli auricolari (ma non me li ero tolti?) una voce insisteva per presentarsi, felice di conoscermi e speranzosa che io potessi indovinare il suo nome. Spensi la musica e raccolsi le penne e il quaderno con scarabocchiati un paio di alberi binari. Ovviamente non c’era traccia dello strano individuo con il bastone e lo sguardo lontano, forse era uscito poco prima. Ricordo di essere uscito di fretta dalla sala insegnanti (credo di essermi dimenticato di firmare sul registro delle uscite, una parentesi lasciata aperta inavvertitamente. Andando verso la classe nella speranza di non incontrare Stern o Brocot per dover spiegare dei loro cassetti (o era un sogno?) indossai la strana sensazione di aver sprecato una preziosa ora buca dietro cose inutili. Devo essere entrato in classe per una noiosissima lezione sul minimo comune multiplo. O almeno credo, perché non ne sono poi così sicuro.
(Mi scuso con lettori e lettrici per questo minuscolo e goffo tentativo, meditato e voluto, di proporre il discorso matematico come argomento di conversazione. L’esigenza nasce da lontano, un’ingombrante necessità di una nuova alleanza culturale. Credo fermamente che in un’epoca di incertezza sia necessario far dialogare tutte le voci, spesso singolari, in un tentativo di discorso plurale. Questo mio diario è probabilmente fallimentare, ma vale come tentativo di ampliare il respiro in opposizione alle tante strettoie di un’epoca a compartimenti. Ringrazio di cuore eventuali scrittori argentini defunti che si sono prestati al gioco.)
Leggi anche:
Riccardo Giannitrapani | Lunedì sono tornato a scuola
Riccardo Giannitrapani | La singolarità
Riccardo Giannitrapani | Le forze di marea
Riccardo Giannitrapani | Orbita di trasferimento
Riccardo Giannitrapani | Il limite di Roche
Riccardo Giannitrapani | Il principio di fragilità







