Diario / Il lemma delle strette di mano
Di nuovo il diario, di nuovo un ricordo. Non leggo più niente, so che adesso la scuola è in bilico, come tutto e tutti. Non voglio che cada, allora lo faccio io per lei. Di nuovo il diario, di nuovo un tentativo di ricordare (raccontare è un orizzonte troppo ampio) la matematica, sponda e rifugio dal reale.
Giovedì sono caduto a scuola. So che può sembrare stupido, goffo o forse patetico, ma mentre salivo trafelato le scale dell’atrio ho sentito un grido di richiamo alle spalle, mi sono distratto e un gradino ha saltato l’appuntamento. Mentre ruotavo scambiando il verticale con l’orizzontale ho anche pensato di essere in realtà fermo, ho immaginato che fosse la scuola a essere caduta, che non avesse retto il colpo di questi mesi e fosse alla fine inciampata. Attaccato alla scuola il terreno, poi la strada, Udine, lo spaziotempo tutto. Ho immaginato la gioia di Ernst Mach nel vedermi fermo e verticale aspettare l’impatto di un intero universo in rotazione mentre i libri che avevo in mano si distanziavano sulle scale seguendo una precisa e parabolica coreografia al rallentatore. A dire il vero non mi sono fatto male, nonostante abbia battuto la testa. Ricordo di aver aspettato un attimo prima di rialzarmi, come a fare un appello mattutino di ossa e orgoglio al posto di studenti.
Ho udito un piccolo fischio fastidioso nel rimettere in piedi la prospettiva, le scale, i corridoi. Strano, ricordo di aver pensato, nessuno in giro. Chi mi ha chiamato facendomi perdere l’equilibrio? E dov’è il personale all’ingresso? Ho raccolto i miei libri dagli scalini e sono andato verso la classe, nemmeno uno studente o una studentessa in giro, nessuna voce, silenzio. Vuoi vedere che ho fatto come due anni fa e sono venuto a scuola di domenica per sbaglio? Ma il portone era aperto, dimostrazione dell’assurdo e per assurdo che non era domenica. E mentre un po’ dolorante e perplesso traslavo verso la mia classe ho avuto paura. Paura di una scuola vuota, di aule vuote, di lavagne vuote, di corridoi vuoti. Niente scarpe, nessuno zaino, nemmeno una mano alzata per andare in bagno, neanche un heyprof sussurrato. Sono arrivato davanti alla porta della 5N, la classe ordinatamente vuota come le altre intraviste in corridoio. Ricordo che ho pensato di essermi sbagliato, non era domenica, era un giorno qualsiasi di un anno qualsiasi, solo che la scuola non c’era più. O forse ero io a non esserci più.

Fu in quel momento che vidi la figura nel corridoio, poco più avanti. Era intenta a guardare con interesse la mappa della scuola con la nuova geografia delle bolle isolate e dei varchi obbligati, una geografia di guerra. In compagnia del fischio dietro l’orecchio mi avvicinai, era una donna di una certa età, vestita in modo bizzarro (anche se adesso non saprei ricordare esattamente i dettagli di quel bizzarro e questa mancanza di memoria lo rende ancora più bizzarro), i capelli bianchi raccolti ed una sigaretta in mano. Aspetta un attimo, come una sigaretta? Avvicinandomi la guardai con un divieto in gola a cui lei rispose con sguardo lontano e voce delicata, quasi un piccolo canto. “Lo so, non dovrei fumare, me lo ha detto anche il dottore. Devo far finta di non aver sentito.” Ricordo di essermi sentito in colpa per i miei modi bruschi, pensando ad una certa distanza (aspetta un attimo, e la mascherina?) che fosse una nuova collega. A dire il vero sembrava aver superato da un pezzo l’età della pensione con quel suo strano sorriso gentile e occhiali sottili sottili. “Forse giovanotto mi può dare una mano. Lei insegna?” Con quel “giovanotto” incastrato nelle orecchie risposi di si, anche se i segni li portavo io e non i miei studenti. Sembrò soddisfatta della risposta e proseguì. “Stavo guardando il modo in cui avete suddiviso la vostra bella scuola, mi sembra di capire che avete quattro zone (che voi chiamate bolle per un motivo che mi sfugge) principali; la sede centrale, dove ci troviamo, il giardino, la palestra e la succursale. Giusto?” “Sì, abbiamo fatto in modo di separare queste zone per avere un controllo accurato di chi entra ed esce. Poi dentro ciascuna bolla abbiamo ulteriori suddivisioni.
Mi scusi, non credo che ci siamo presentati, stavo cercando la mia classe ma effettivamente non è in aula. Effettivamente non c’è nessuno in giro. Posso chiederle lei chi è?” “Una donna curiosa, essenzialmente. Mi dica, queste zone, queste bolle, sono collegate da questi passaggi che qui sono indicati come varchi, giusto? Che cosa complicata, non potevate lasciare aperto tutto a tutti?” Domandandomi dove fosse stata negli ultimi sette mesi cercai di spiegarle con pazienza che lo scopo dei varchi tra le bolle era di controllare, appunto, il passaggio da una zona all’altra. “Sa, il virus…” Mi guardò come se avessi parlato in polacco. “Giovanotto, deve aver pazienza, sono una donna curiosa ma anche un po’ avanti con gli anni, questa mappa è troppo dettagliata, troppo complicata.” Tirai fuori il mio quaderno degli appunti e scarabocchiai una versione schematica della mappa.
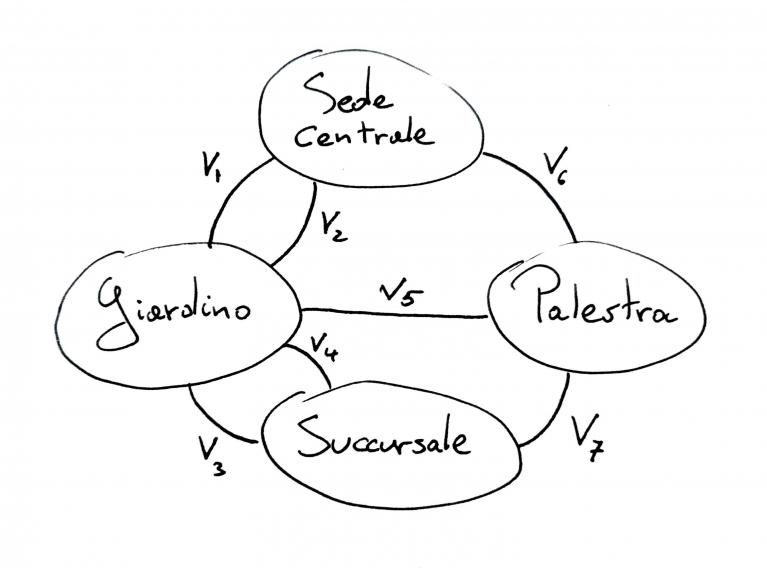
“Ecco, vede? In realtà è molto semplice, ridotta all’essenziale la mappa è quella che i matematici chiamano un grafo.” “Un grafico? Non sembra affatto un grafico, scusi se glielo dico.” Sospirai, il fischio della caduta costante nell’orecchio. “No, non grafico, grafo. In breve è un insieme di elementi detti nodi con dei collegamenti detti archi. Nel nostro caso i nodi sono le bolle (la sede centrale, la palestra, il giardino e la succursale) e gli archi sono i varchi che collegano le bolle, qui li ho indicati con v1, v2, v3 etc. Sono sette in tutto.” “Capisco. Come mai ci sono due varchi tra la sede centrale e il giardino, per esempio? Non ne bastava uno solo?” “Così possiamo dividere le classi quando le portiamo fuori e non devono passare tutte dallo stesso varco. Sa, per il distanziamento, no?” “Sì sì, certo.” Sembrò per un attimo distratta ad ascoltare una voce interiore. Poi con un sorriso mi guardò forse per la prima volta. “Senta, giovanotto. Visto che lei non trova la sua classe e quindi avrà del tempo da perdere, che ne dice di accompagnarmi a visitare la sua bella scuola? Così potrò vedere tutti questi nodi e passare attraverso tutti questi varchi. Le ho già detto che sono una donna curiosa. E poi colleziono cianfrusaglie, magari in questo piccolo giro trovo un ricordo di questa passeggiata. Che ne dice? Le va? Almeno per oggi che c’è tutto questo silenzio, almeno per oggi che non sentiamo il fragore delle macchine che tritano la carta.”
Pensai alla 5N che non era in classe, ai corridoi vuoti, alle scarpe assenti (le devo segnare sul registro? Ci sarà un appello delle scarpe da qualche parte?), pensai alla mia caduta ed alla caduta della scuola, pensai che non volevo restare solo in quel luogo silenzioso. Accettai. “Bene, sono contenta. E mi dica, riusciamo a fare questa piccola passeggiata in modo da passare attraverso tutti i varchi? Sono proprio curiosa di vederli tutti.” “Beh, sì, certo, possiamo farlo, ma dovremo passare più volte dallo stesso varco, si annoierà.” “Mi sta dicendo, giovanotto, che non c’è modo di fare una passeggiata che passi attraverso tutti i varchi una e una sola volta? E se io provassi lo stesso?” “Certo che può, ma non ci riuscirà. Provi pure qui sulla mappa a trovare un percorso che passi attraverso tutti i varchi senza mai usare un varco più di una volta, le assicuro che non è possibile. Le posso chiedere però per favore di non chiamarmi giovanotto?” “Certo giovanotto che può chiedermelo, ma lei mi ricorda tanto mio nipote Königsberg, anche lui ha l’aspetto goffo. In ogni caso sembra che lei abbia ragione, ogni volta che ci provo mi tocca passare su un varco dove sono già passata. Mi dica la verità, ci ha provato anche lei in passato? Ma saprebbe dimostrare questa sua affermazione con sicurezza? Magari ci sta sfuggendo un particolare percorso che nessuno dei due ha visto. Può veramente dimostrarmi che nessuna passeggiata riesce a passare una e una sola volta da ciascun varco? Le dobbiamo cercare tutte, una faticaccia temo.” Risposi con sicurezza. “Non lo devo dimostrare io, ci ha pensato Eulero, parecchio tempo fa. E lo spirito di una dimostrazione matematica è proprio quello di far vedere qualcosa senza bisogno di provare tutti i casi possibili. Vede, se devo camminare senza mai usare lo stesso varco più di una volta, significa che quando arrivo ad un nodo attraverso un arco non posso usare lo stesso arco per uscire da quel nodo. Quindi ogni volta che nella mia passeggiata tocco un nodo devo avere un arco per entrare ed uno per uscire distinti. Due varchi. Un nodo lo posso toccare anche più volte, ma ogni volta devo avere due archi distinti, uno per entrare e uno per uscire. In altre parole ogni nodo deve avere un numero di archi multiplo di due, cioè pari. A questa condizione fanno eccezione il nodo di partenza e quello di arrivo dove gli archi possono anche essere dispari in quanto quando parto sono già nel nodo e quando arrivo non devo uscire più.”
Rimase a lungo senza parlare, gli occhiali spalmati sul mio quaderno ed il piccolo schema scarabocchiato sopra. “Credo di aver capito. In questa mappa, o meglio grafo come piace chiamarlo a lei, tutti i nodi sono dispari, quindi non è soddisfatta questa regola che lei mi ha appena illustrato.” “Esatto.
Perché in un grafo ci possa essere un cammino che tocchi tutti gli archi senza mai passare due volte per lo stesso arco (un tale cammino si chiama appunto euleriano), tutti i nodi devono essere toccati da un numero di archi pari, tutti tranne al più due, il nodo di partenza ed il nodo di arrivo. Per inciso, il numero di archi che tocca un nodo si chiama grado del nodo; la mappa della nostra scuola ha tutti i nodi di grado dispari, come lei ha notato, quindi non ammette un cammino euleriano.” “La ringrazio, davvero, è stato molto gentile. Che ne dice adesso di accompagnarmi in giardino? Tutto questo parlare di passeggiate stando fermi mi sembra un’assurdità. Non dico di aver capito tutto tutto (che poi tutto è solo una parola sfrontata), ma sicuramente mi ha regalato qualcosa a cui pensare.” Ci incamminammo silenziosi e attraverso uno dei varchi spuntammo in giardino, un orizzonte di foglie rosse e alberi e grigio cielo ad attenderci. Mi accorsi di non avere più paura, che la scuola in qualche modo non era più vuota, come se parlare potesse sostituirsi alle persone, come se le parole potessero prendere il posto di studenti e studentesse, del personale e degli insegnanti, una moltitudine di parole presenti, sedute ai banchi, in piedi alla lavagna, una smisurata scuola di parole.
“Abbia pazienza, giovanotto, mi sono venute in mente due cose da aggiungere a tutto il discorso fatto, posso abusare della sua pazienza?” “Certo, mi piace parlare di queste cose, mi fa sentire meno solo in questa strana mattinata. Dica pure.” “Bene, la prima è che se io potessi togliere un solo varco, per esempio il passaggio dal giardino alla palestra, ecco che un percorso euleriano (così lo ha chiamato, giusto) diventa possibile. Infatti i nodi diventano di grado pari (tranne due che rimangono di grado dispari ma che posso usare per la partenza e l’arrivo) e la condizione che mi ha gentilmente enunciato è soddisfatta. Se mi presta gentilmente il suo taccuino le faccio vedere.” Disegnò un nuovo schema più o meno come questo.
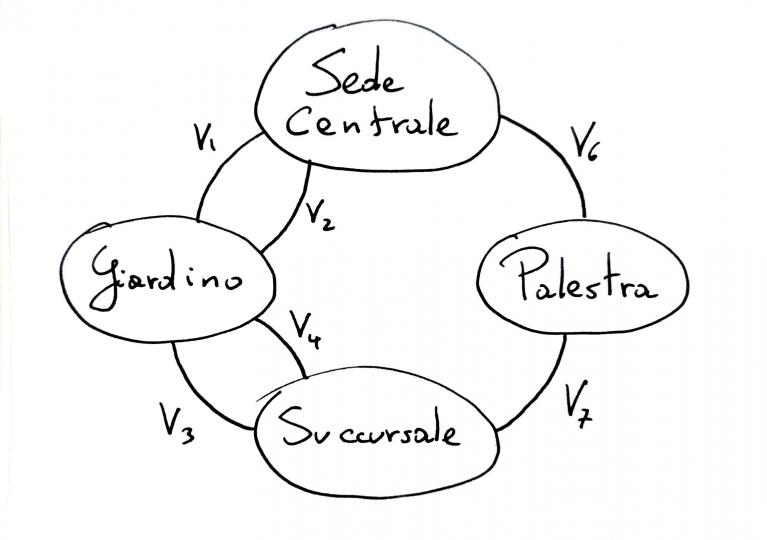
“Sì, ha perfettamente ragione, avendo tolto il varco v5 adesso sia il giardino che la palestra hanno un numero pari di varchi e in questo modo è possibile un cammino che passi per ogni varco una sola volta. Anzi, più di uno. Siccome però la sede principale e la succursale hanno ancora un numero dispari di varchi, la condizione è che si parta da uno di questi due edifici e si arrivi nell’altro.” “Bene, sono contenta di aver capito questo gioco dei grafi. Certo che è interessante, eliminando solo un arco cambia completamente l’essenza del grafo, si passa da uno dove una cosa è impossibile ad uno dove invece si può fare.” “Sì, in effetti questo è il bello e la ricchezza dei sistemi interconnessi che sono rappresentati dai grafi. Un piccolo cambiamento, magari in apparenza marginale, cambia completamente la struttura globale.” “Un po’ come le società fatte di persone, di sentimenti, di amore, di odio, di invidia e altruismo. Alle volte sono i piccoli cambiamenti, le insospettabili e minuscole modifiche che hanno ripercussioni enormi. Guerra o pace, ordine o caos.” “Sì, per questo la topologia dei grafi è un universo affascinante della matematica. Ma qual è la seconda cosa che le è venuta in mente?” “Ah, sì, giusto. Ho notato che sia nel primo grafo, quello da cui siamo partiti, sia nel secondo che le ho disegnato poco fa con un arco in meno, la somma di tutti i gradi dei nodi è sempre pari.
Nel primo caso è 14 e nel secondo 12. Si tratta di un caso o questa proprietà vale per ogni grafo?” “Sì, esatto, lei ha appena enunciato il cosiddetto lemma delle strette di mano, le lascio capire da sola perché si chiama in questo modo strano e particolarmente fuori luogo visto il periodo storico che stiamo vivendo, ci vorrebbe un lemma del saluto a distanza. In ogni caso non è difficile da dimostrare e vale per ogni grafo (almeno del tipo di cui stiamo parlando), la somma di tutti i gradi dei nodi è sempre pari. Un indizio per la dimostrazione, se ha voglia di pensarci: ogni volta che tolgo o aggiungo un arco in un grafo diminuisco o aumento di uno il grado di due nodi. Non le dico di più per non rovinarle la sorpresa della dimostrazione, le dico solo che questo lemma ha una conseguenza che possiamo verificare sui nostri due grafi: il numero di nodi di grado dispari deve essere pari.” “Va bene, mi piacciono le sfide, ma non ora, il suo sembra più uno scioglilingua che un teorema. E poi lei giovanotto ha una classe da ritrovare e io sono piuttosto stanca. Sono contenta di questa chiacchierata, ci siamo incrociati come estranei, doveva accadere. Ma ora mi piacerebbe sedermi su questa panchina a ripensare un po’ alla nostra conversazione. Magari guardo un po’ il cielo, non finisce mai di stupirmi. Ora vada che credo sia tardi per lei. Le stringerei volentieri la mano, ma la vedo titubante; non importa, le strette di mano, che siano zero, due o una moltitudine, sono sempre pari, ce lo garantisce il lemma di cui mi ha parlato. Che conforto la matematica con le sue imprecise certezze.”
Ricordo di averla salutata con un velo di tristezza, a distanza di giorni non ho ancora capito chi fosse e come mai fosse tanto interessata a mappe, grafi e cammini. Ma ricordo di essere tornato dentro senza voltarmi, il ronzio della caduta ancora aggrappato all’orecchio, sperando di trovare la mia 5N, pensando alla topologia della scuola, alla sua fragilità, al numero enorme di archi che connettono studenti e studentesse, insegnanti e personale, famiglie e società; nodi con il loro carico di imperfezione e umanità, con i loro sogni, aspettative, delusioni. Non può esistere una scuola vuota, nonostante tutto. Al più si possono svuotare gli edifici, i corridoi, le aule, si possono smontare le lavagne e far tacere le campanelle; la scuola è da un’altra parte per fortuna.
Nel vuoto dell’ingresso ricordo di essermi fermato un attimo a riordinare le idee, abbandonando ogni tentativo di trovare qualcuno, stanco di cercare un cammino che passi una ed una sola volta per ciascun varco. Fu in quel momento che intravidi un movimento sulle scale, la corsa veloce di un collega in ritardo, l’aria stranamente familiare. Con il fischio nell’orecchio ormai diventato insopportabile, urlai per avvertirlo. Fu inutile, lo vidi inciampare sulle scale spargendo libri in una precisa e parabolica coreografia al rallentatore.
(Ogni riferimento a eventuali poetesse polacche defunte è voluto, cercato, desiderato.)
Leggi anche:
Riccardo Giannitrapani | Lunedì sono tornato a scuola
Riccardo Giannitrapani | La singolarità
Riccardo Giannitrapani | Le forze di marea
Riccardo Giannitrapani | Orbita di trasferimento
Riccardo Giannitrapani | Il limite di Roche
Riccardo Giannitrapani | Il principio di fragilità
Riccardo Giannitrapani | L'albero di Calkin Wilf







